Hukum Kirchoff

Hukum Kirchoff I 

Pada pertengahan abad 19 seorang fisikawan asal Jerman, Gustav Kirchoff (1824-1887) berhasil menemukan metode untuk menentukan arus yang mengalir pada rangkaian listrik bercabang. Penemuan Kirchoff tersebut dikenal sebagai hukum Kirchoff I dan hukum Kirchoff II. Pada topik ini, kalian hanya akan belajar tentang hukum Kirchoff I.
        Hukum kirchoff I biasa disebut sebagai hukum titik cabang karena hukum ini tidak diterapkan pada rangkaian loop tertutup. Namun, diterapkan pada rangkaian yang memiliki banyak cabang. Hukum kirchoff I sering dianalogikan dengan laju aliran pada sebuah pipa air. Jika pada pipa tersebut tidak terjadi kebocoran, maka jumlah air yang masuk sama dengan jumlah air yang keluar. Pernyataan hukum Kirchoff I adalah “jumlah kuat arus yang masuk dalam suatu titik percabangan sama dengan jumlah kuat arus yang meninggalkan titik percabangan tersebut”. Secara matematis, persamaan hukum Kirchoff I dapat dinyatakan sebagai berikut.

$\sum I_{masuk}=\sum I_{keluar}$

Persamaan di atas menunjukan bahwa, jumlah kuat arus listrik yang masuk sama dengan jumlah kuat arus listrik yang keluar. Berikut ini merupakan ilustrasi percabangan arus berdasarkan hukum Kirchoff I.

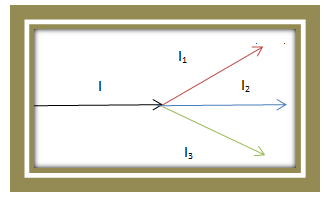
        Berdasarkan persamaan sebelumnya, hukum kirchoff I ini dapat digunakan untuk menghitung jumlah kuat arus listrik yang melalui suatu titik percabangan. Hukum kirchoff I biasa disebut hukum kekekalan muatan karena muatan yang mengalir di dalam rangkaian tidak berubah. Hal ini menunjukkan bahwa, laju muatan (kuat arus) yang menuju titik cabang sama dengan laju muatan (kuat arus) yang meninggalkan titik cabang.

Contoh Soal

Perhatikan gambar titik percabangan kuat arus berikut ini.

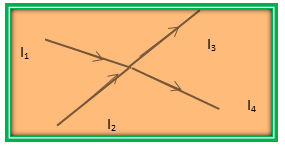
Jika kuat arus listrik pada I1 = 2A, I2 = 6 A dan I3 adalah 4 A, maka berapakh kuat arus yang mengalir pada I4 ?
Penyelesaian
Diketahui:
I1 = 2 A
I2 = 6 A
I3 = 4 A
Ditanyakan: I4 ?
Jawab:

$\sum I_{masuk}=\sum I_{keluar}$

$I_1+I_2=I_3+I_4$

$2+6=4+I_4$

$8-4=I_4$

$I_4=4$ A

Jadi, kuat arus listrik pada I4 adalah 4 A.

Hukum Kirchoff II

 Hukum Kirchoff I memuat metode untuk menghitung kuat arus dalam rangkaian listrik bercabang, sedangkan hukum Kirchoff II memuat metode untuk menghitung jumlah tegangan pada suatu lintasan tertutup. Hukum Kirchoff II menyatakan bahwa “pada suatu rangkaian tertutup (loop), jumlah aljabar dari gaya gerak listrik (potensial listrik) dan penurunan tegangannya sama dengan nol.” Secara matematis, dapat dirumuskan sebagai berikut.

$\sum \epsilon +\sum IR=0$

Keterangan:
ε = gaya gerak listrik (V);
I = kuat arus listrik (A); dan
R = hambatan listrik (Ohm).

Berdasarkan persamaan di atas, jumlah aljabar potensial listriknya sama dengan nol. Hal itu menunjukkan bahwa, tidak ada energi listrik yang hilang dalam rangkaian tersebut, sehingga dasar perumusan hukum Kirchoff II adalah kekekalan energi. Perjanjian tanda untuk ggl (ε) dan kuat arus (I) dalam persamaan di atas adalah sebagai berikut.
a. Kuat arus bertanda positif jika searah dengan arah loop dan negatif jika berlawanan dengan arah loop.
b. Apabila menjumpai kutub positif, maka gglnya bertanda positif dan berlaku sebaliknya.
        Penggunaan hukum Kirchoff II ini hanya berlaku pada rangkaian tertutup. Jika ada rangkaian listrik yang terdiri dari beberapa rangkaian tertutup, maka analisisnya menggunakan rangkaian tertutup satu per satu. Hukum ini juga digunakan untuk menentukan suatu tegangan sumber yang belum diketahui arus atau hambatannya.

Hukum Kirchoff II untuk 1 Loop

Contoh rangkaian tertutup 1 loop ditunjukkan oleh gambar berikut.

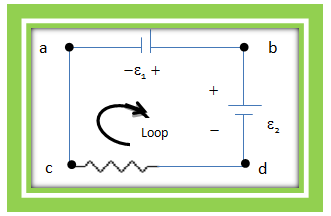
Gambar di atas merupakan contoh rangkaian 1 loop tertutup yang terdiri dari dua buah sumber tegangan dan satu komponen hambatan. Pada rangkaian tersebut, arus listrik yang mengalir dalam rangkaian sama, yaitu I. Untuk mendapatkan penyelesaian rangkaian tertutup tersebut, berikut ini langkah-langkahnya.

1. Buatlah loop pada rangkaian tersebut dan tentukan arahnya, misalnya kalian memilih loop abcda.
2. Arus yang searah dengan arah loop bernilai positif dan sebaliknya jika berlawanan arah loop dianggap negatif
3. Gunakan aturan loop untuk menentukan beda potensial setiap elemen. Aturan loop tersebut adalah sebagai berikut.

a. Jika loop bergerak dari a ke b (searah dengan arus dan melewati sebuah hambatan), maka terjadi perubahan potensial -IR.

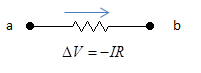
b. Jika loop bergerak dari a ke b (berlawanan dengan arah arus dan melewati sebuah hambatan), maka terjadi perubahan potensial IR.

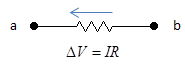
c. Jika loop bergerak dari a ke b (melewati ggl listrik dari kutub negatif ke kutub positif), maka terjadi perubahan potensial ε.
d. Jika loop bergerak dari a ke b (melewati ggl listrik dari kutub positif ke kutub negatif), maka akan terjadi perubahan potensial –ε.

4. Jumlahkan beda potensial pada setiap elemen dalam loop, kemudian gunakan rumus ΔV = 0, sehingga diperoleh besaran listrik yang ingin diketahui.

Hukum Kirchoff II untuk 2 Loop

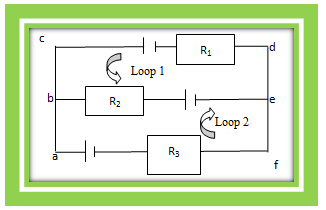
Rangkaian yang memiliki dua loop atau lebih disebut juga rangkaian majemuk. Langkah-langkah dalam menyelesaikan rangkaian majemuk ini adalah sebagai berikut.

1. Tentukan arah loop yang dipilih.
2. Tentukan arah kuat arus listrik pada tiap titik percabangan.
3. Tulislah persamaan-persamaan arus untuk tiap titik cabang menggunakan hukum Kirchoff I.
4. Tuliskan persamaan-persamaan pada setiap loop menggunakan persaman hukum Kirchoff II.
5. Hitunglah besaran-besaran yang ditanyakan menggunakan metode eliminasi atau subtitusi.

Contoh Soal

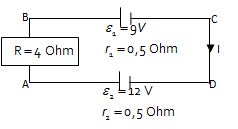
Jika titik A ditanahkan, berapakah kuat arus yang melalui rangkaian?
Penyelesaian
Diketahui:
R = 4 Ohm
ε1 = 9 V
r1 = 0,5 Ohm
ε2 = 12 V
r2 = 0,5 Ohm
Ditanyakan: I ?
Jawab:

$\sum \epsilon +\sum IR=0$

${\epsilon }_1-{\epsilon }_2+I\left(R+r_1+r_2\right)=0$

$I=\frac{{\epsilon }_2-{\epsilon }_1}{R+r_1+r_2}=\frac{12-9}{4+0,5+0,5}$

$I=\frac{3}{5}=0,6$ A

Jadi, kuat arus yang mengalir dalam rangkaian adalah 0,6 A.