Pembahasan Soal Momen Inersia

 

UN 2013

Dua bola masing-masing massanya m₁ = 2 kg dan m₂ = 3 kg dihubungkan dengan batang ringan tak bermassa seperti pada gambar.

Jika sistem bola diputar pada sumbu di titik a, besar momen inersia sistem bola adalah ….

A.   0,24 kg.m²
B.   0,27 kg.m²
C.   0,30 kg.m²
D.   0,31 kg.m²
E.   0,35 kg.m²

Pembahasan

diketahui :

m₁ = 2 kg 
m₂ = 3 kg 
R₁ = 20 cm = 0,2 m 
R₂ = 30 cm = 0,3 m

Ditanyakan Momen inersia (I) pada sistem tersebut adalah...

Solusi

I = ΣmR²
  = m₁R₁² + m₂R₂²
  = 2 × 0,2² + 3 × 0,3²
  = 0,08 + 0,27
  = 0,35

Jadi, besar momen inersia sistem bola tersebut adalah 0,35 kg.m² (E).

UN 2013

Dua bola dihubungkan dengan kawat yang panjangnya 6 m seperti pada gambar.

Massa kawat diabaikan dan kedua bola diputar dengan sumbu putar tegak lurus kawat pada benda m₁. Besar momen inersia sistem adalah ….

A.   6 kg.m²
B.   18 kg.m²
C.   36 kg.m²
D.   54 kg.m²
E.   72 kg.m²

Pembahasan

Pada sistem tersebut sumbu putarnya adalah m₁, berarti momen Inersia m₁ adalah 0.

Sehingga..
I = m₂R₂²
  = 2 × 6²
  = 2 × 36
  = 72

Jadi, momen inersia sistem tersebut adalah 72 kg.m² (E).

UNAS 2008

Batang AB massanya 2 kg diputar melalui ujung A ternyata momen inersianya 8 kg.m².

Bila diputar melalui pusat O (AO = OB), momen inersianya menjadi ….

A.   2 kg.m²
B.   4 kg.m²
C.   8 kg.m²
D.   12 kg.m²
E.   16 kg.m²

Pembahasan

Saat batang AB diputar dengan poros A, momen inersianya 8 kg.m², sehingga panjang batang R dapat dicari dengan rumus: 

I = mR²
8 = 2R² 
R² = 4 
R = 2 m

Saat batang AB diputar dengan poros A, massa batang terbagi menjadi dua, demikian juga jarak terhadap poros: 

m_A = 1 kg 
m_B = 1 kg 
R_A = 1 m 
R_B = 1 m

Dengan demikian, momen inersianya menjadi: 

I = ΣmR²
  = m_AR_A² + m_BR_B²
  = 1 × 1² + 1 × 1²
  = 1 + 1
  = 2

Jadi, momen inersia pada keadaan tersebut adalah 2 kg.m² (A).

UN 2015

iga benda P, Q, dan R terletak pada bidang x-y yang saling dihubungkan dengan batang tipis dan ringan membentuk sistem benda tegar.

Data benda diberikan pada tabel:

Benda	Massa (kg)	Koordinat (meter)
P	1	(0, 3)
Q	2	(4, 0)
R	1	(0, −3)

Sistem diputar pada poros yang menembus bidang melalui benda Q dan tegak lurus bidang gambar, maka besar momen inersia sistem adalah ….

A.   50 kg.m²
B.   40 kg.m²
C.   20 kg.m²
D.   15 kg.m²
E.   5 kg.m²

Pembahasan

Karena benda Q bertindak sebagai sumbu putar maka yang diperhitungkan hanya benda P dan R. Perhatikan gambar berikut.

Berdasarkan gambar di atas, momen inersia sistem tersebut adalah:

I = m₁ R₁² + m₂ R₂²
  = 1 ∙ 5² + 1 ∙ 5²
  = 25 + 25
  = 50

Jadi, besar momen inersia sistem tersebut adalah 50 kg.m² (A).

UN 2016

Perhatikan gambar empat partikel yang dihubungkan dengan batang penghubung berikut!

Massa m₁ = m₂ = 4 kg dan m₃ = m₄ = 2 kg, panjang a = 1 meter dan b = 2 meter, serta massa batang penghubung diabaikan. Momen inersia sistem partikel terhadap sumbu y adalah ....

A.   24 kg.m²
B.   32 kg.m²
C.   34 kg.m²
D.   56 kg.m²
E.   60 kg.m²

Pembahasan

Misalkan jarak antara partikel terhadap sumbu y adalah R, maka: 

R₁ = 2a
     = 2 × 1 meter
     = 2 meter  

R₂ = a
     = 1 meter 

R₃ = b
     = 2 meter 

R₄ = 2b
     = 2 × 2 meter
     = 4 meter

Momen inersia sistem partikel tersebut adalah:

I = ∑mR²
  = m₁R₁² + m₂R₂² + m₃R₃² + m₄R₄²
  = 4×2² + 4×1² + 2×2² + 2×4²
  = 16 + 4 + 8 + 32
  = 60  kg.m²

Jadi, momen inersia sistem partikel terhadap sumbu y adalah   60 kg.m² (E).

UN 2017

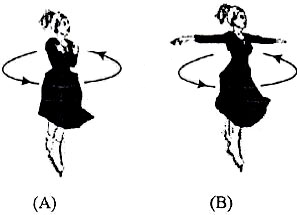
Seorang penari berdiri di atas lantai es licin dan berputar di tempatnya seperti pada gambar.

Mula-mula penari tersebut berputar dengan menyilangkan kedua tangan di dadanya (gambar A). Kemudian penari tersebut kembali berputar sambil merentangkan kedua tangannya (gambar B). pernyataan pada tabel di bawah ini yang benar berkaitan dengan kedua keadaan penari di atas adalah ….

	Momen inersia (I)	Momentum sudut (L)
A.	IA = IB	LA < LB
B.	IA > IB	LA = LB
C.	IA > IB	LA > LB
D.	IA < IB	LA < LB
E.	IA < IB	LA = LB

Pembahasan

Hubungan antara momen inersia dengan momentum sudut dirumuskan sumbu:

L = I ω

Momentum sudut bersifat kekal. Sehingga momentum sudut penari yang berputar dengan tangan disilangkan (L_A) sama dengan momentum sudut saat berputar dengan kedua tangannya direntangkan (L_B).

L_A = L_B

Sedangkan momen inersia nilainya bergantung pada jarak atau jari-jari putar sesuai rumus:

I = mR²

Jari-jari putar penari dengan kedua tangan disilangkan (R_A) lebih kecil dengan jari-jari putar penari saat kedua tangannya direntangkan (R_B).

R_A < R_B

Karena momen inersia berbanding lurus dengan jari-jari putar maka:

I_A < I_B

Jadi, pernyataan pada tabel di atas yang benar adalah opsi (E).